Проблемы Эволюции

А.В.Марков, Е.Б.Наймарк. М.: Геос, 1998. 318 с.

Количественные закономерности макроэволюции

Глава 2

Модель эволюции надвидового таксона

2.1. Общие замечания

В качестве первого шага или отправной точки в исследовании надвидовых таксонов как развивающихся систем целесообразно предложить более или менее простую имитационную модель, в которой бьши бы учтены основные положения системной концепции таксонов. Такая модель разработана авторами [Марков, Наймарк, 1994в, 1996а; Марков, 1996].

К настоящему времени предложено немало моделей, описывающих те или иные аспекты эволюционного процесса. Однако большинство этих моделей затрагивает преимущественно микроэволюционные механизмы, которые здесь не рассматриваются. Так, во многих эволюционных моделях используются следующие основные принципы: 1) эволюционирующий вид (или организм) описывается конечным числом морфологических признаков, так или иначе градуированных; 2) признаки изменяются, случайно и ненаправленно (таким образом имитируется мутационный процесс); 3) иногда в моделях задается структура ниш или лицензий и вектор приспособленности, организующий определенным образом случайные изменения. Модели, построенные таким образом, рассматриваются в ряде работ [Меншуткин, 1977, 1988; Valentine, Walker, 1986; Минчич, 1987; Меншуткин, Левченко, 1988; Букатова, 1994].

Результатом реализации таких моделей обычно является достижение модельным таксоном максимально возможного разнообразия и его стабилизация на этом уровне. Если в модели вместо матрицы признаков (или экологических ниш) задаются скорости вымирания и появления, то в зависимости от соотношения этих скоростей динамика разнообразия либо описывается куполообразной кривой [Raup, 1978], либо устанавливается уровень стабильного разнообразия [Raup, Valentine, 1983].

В качестве предшественников модели, описанию которой посвящена эта глава, отчасти можно рассматривать математические модели коэволюции видов [Levin, 1971; Leon, 1974; Lawlor, Maynard Smith, 1976], в которых основное внимание уделяется механизмам конкуренции и конкурентного вытеснения (в нашей модели эти механизмы учитываются, но не имитируются в деталях и не составляют основного содержания модели). Можно упомянуть также ряд моделей таксономической диверсификации [Sepkoski, 1979; Miller, Sepkoski, 1988; Kitchell, Carr, 1985], в которых заложены отдельные элементы системного понимания эволюции таксонов в единой адаптивной зоне (диверсификация таксона ограничивается диверсификацией экологически близких таксонов).

Предлагаемая здесь имитационная модель отличается от предшествующих аналогов тем, что она опирается на системную концепцию высших таксонов. В некотором смысле она является дальнейшим развитием предложенной В.В.Черныхом [1986] модели ансамблевого развития родственных видов. Одной из задач моделирования была проверка основных положений системной концепции. Предполагается, что сравнение эволюции модельного таксона с эволюцией естественных групп дает возможность оценить адекватность теоретических предпосылок модели реальным причинно-следственным связям.

Предлагаемая модель заведомо упрощает реальную картину, о чем будет подробно сказано ниже (гл. 3). Очевидно, что на этом начальном этапе исследований определенные упрощения необходимы и неизбежны. По мнению И.Я.Павлинова [1992а, с. 229-230], при разработке эволюционных моделей "одно из основных требований -разрабатывать такие модели, которые давали бы возможность выдвигать строго тестируемые гипотезы. С этой точки зрения чем проще модель, тем она предпочтительнее как более конструктивная, поскольку содержит меньше непроверяемых ad hoc допущений о свойствах исторического развития".

Для удобства изложения и восприятия материала в данном случае целесообразно обсуждение теоретических предпосылок модели дать после ее описания.

2.2. Описание модели

Модель имитирует процессы появления и вымирания субъединиц таксона надвидового (условно - семейственного) ранга. В модели не предусмотрены критерии точного определения ранга таксона. Поэтому модельный таксой можно назвать и родом, и отрядом и т.д. Основным понятием, используемым для построения модели, является понятие адаптивной зоны. Адаптивной зоной таксона считается разнообразие условий, которое потенциально устроило бы представителей таксона, или объем той области пространства ресурсов, в которой потенциально возможно существование представителей данного таксона (см. раздел "Терминология"). Такое понимание адаптивной зоны в общем согласуется со взглядами других авторов [Симпсон, 1948; Van Valen, 1971; Шмальгаузен, 1983; Северцов, 1987а], при этом в предлагаемой модели акцентируется возможность неполного использования таксоном своей адаптивной зоны, которая понимается именно как потенциальное, а не реальное жизненное пространство. Главным исходным параметром, задаваемым в начале работы модели, является размер адаптивной зоны семейства (константа Az). Очевидно, что в природе размеры адаптивной зоны таксона могут изменяться под воздействием внешних факторов. Так, регрессии, похолодания, развитие конкурирующих групп являются факторами, приводящими к сжатию адаптивной зоны таксона бен-тосных животных. Трансгресии, потепления и вымирание конкурирующих групп могут расширять эту адаптивную зону. Однако, по всей видимости, в истории многих групп имелись длительные периоды, когда размеры их адаптивных зон оставались примерно постоянными. Поэтому в модели величина адаптивной зоны семейства полагается постоянной, хотя имеется возможность произвольного изменения этой величины в ходе реализации модели. Следует различать потенциальное (максимально возможное) экологическое пространство семейства (константа Az) и реально занимаемое (переменная А). Объем реально занимаемых экологических ниш {А) в модели непрерывно меняется в зависимости от текущего числа родов (n) и размеров родовых экологических ниш (a_i). Разность между потенциальной адаптивной зоной и ее реализованной частью характеризует текущий объем свободного (незанятого) экологического пространства в адаптивной зоне семейства (Атах):

Атах = Az-A

Вторым исходным понятием модели является минимальное экологическое пространство, необходимое для существования модельного рода, которое выражается постоянной Amin.

Модельное семейство состоит из родов. Каждый i-ый модельный род описывается двумя характеристиками:

1.Размером адаптивной зоны рода (константа az_i ). Она отражает потенциальное экологическое пространство, которое может быть занято родом. Величина az_i не может превышать Az.

2. Размером реализованной части адаптивной зоны рода, или текущим объемом экологической ниши, занимаемой родом - переменная a_i. Сумма занимаемых ниш всех родов семейства не может превышать величину адаптивной зоны семейства:

В противном случае произойдет как бы образование нового семейства, что в данной модели не предусматривается. С другой стороны, величина реализованной части адаптивной зоны рода (a_i) не может быть меньше Amin, поскольку в этом случае род оказывается нежизнеспособным, т.е. оставшееся в его распоряжении жизненное пространство недостаточно для поддержания существования рода. Размер экологической ниши, занимаемой родом, есть мера экологической специализированноести рода: небольшая a_i соответствует специализированным родам, тогда как роды-генералисты имеют большую величину a_i.

Блок-схема модели изображена на рис. 11. Модельное семейство обозначается на рисунке кругом, площадь которого соответствует размеру адаптивной зоны семейства (Az). Роды символизируются секторами круга. Площадь сектора - адаптивная зона рода (az_i). Заштрихованная часть сектора изображает реализованную часть адаптивной зоны рода (a_i). Вся незаштрихованная площадь круга составляет в совокупности свободное экологическое пространство (Атах). На схеме показана последовательность моделируемых эволюционных событий, происходящих с одним из родов. Для удобства этот род на рисунке изображен самым большим сектором.

Рис. 11.

Блок-схема имитационной модели эволюции надвидового таксона (пояснения в тексте)

Fig. 11. Scheme of the simulation model of the evolution of a high taxon

В модельном семействе происходят четыре основных эволюционных процесса:

1. Экстенсивная дивергенция.

Под этим термином подразумевается возникновение новых родов путем выхода в незанятую часть адаптивной зоны семейства. В результате экстенсивной дивергенции род-предок не исчезает и его характеристики остаются прежними. Новый род, образно говоря, отпочковывается от старого, уходя в новую нишу. Предполагается, что вероятность экстенсивной дивергенции (переменная Pext) положительно зависит как от a_i предка, так и от Атах. Это означает, что узкие специалисты имеют меньше шансов освоить новую среду обитания, чем неспециализированные формы. Кроме того, вероятность экстенсивной дивергенции тем выше, чем больше незанятого экологического пространства имеется в данный момент в адаптивной зоне семейства. Последнее утверждение соотносится с известным фактом, что в начале истории многих групп очень быстро возникают целые букеты новых таксонов, затем образование новых таксонов, в особенности неспециализированных, приостанавливается .

Вероятность экстенсивной дивергенции 0<Pext<1. Верхний предел Pext, по всей вероятности, специфичен, т.е зависит от характеристик конкретной группы, обозначим этот предел т2. Ясно, что т2 тоже изменяется от 0 до 1. Целесообразно предположить, что наличие свободного пространства и специализация могут по-разному влиять на ход экстенсивной дивергенции у разных групп, это различие отражается параметром k2. Простейшая функция, учитывающая все перечисленные условия, следующая:

Pext = m2*Amax*a_i^k5/(Amax*a_i^k5 + k2)

где a_i - размер экологической ниши, занимаемый родом-предком; т2, k2 - коэффициенты, k5 - параметр, указывающий в какой степени экологическая специализация предковой формы препятствует появлению неспециализированных потомков.

После вычисления вероятности экстенсивной дивергенции принимается решение о том, произойдет ли от i-того рода экстенсивным путем новый род. Эта операция моделируется как эксперимент с ящиком Бернулли.

Если экстенсивная дивергенция осуществляется, то задается величина адаптивной зоны нового рода (az_i). Она задается как случайное число в диапазоне от 0 до Атах. Размер экологической ниши, т.е. реализованная часть адаптивной зоны, занимаемая новым родом (a_i), задается случайным числом в диапазоне от 0 до величины адаптивной зоны этого рода (az_i). Если величина a_i оказывается при этом меньше Amin, то новый род признается нежизнеспособным, и дивергенция не происходит. В противном случае появляется род с указанными параметрами. После этого величина свободного экологического пространства в адаптивной зоне семейства (Атах) пересчитывается: от старого значения отнимается величина a_i вновь появившегося рода.

2. Интенсивная дивергенция:

возникновение двух новых родов на месте одного старого путем дробления исходной ниши. Род-предок замещается двумя родами, которые делят между собой адаптивную зону и экологическую нишу предка. Для тех количественных показателей, которые анализируются на выходе модели (см. конец раздела 2.2.), не важно, считать ли род-предок исчезнувшим или рассматривать один из двух "новых" родов как продолжение рода-предка. Вероятность интенсивной дивергенции повышается по мере заполнения адаптивной зоны семейства: чем меньше Атах, тем выше вероятность появления экологически специализированных форм. Верхний предел варьирования вероятности интенсивной дивергенции задается параметром тЗ (0<m3<1). Форма зависимости величины Pint от размеров свободного экологического пространства регулируется параметром k3. В простейшем виде все эти ограничения учитываются функцией:

Pint = m3 / (k3*Amax + 1)

где тЗ и k3 - коэффициенты.

Принятие решения об осуществлении интенсивной дивергенции после определения вероятности этого события происходит так же, как и в случае экстенсивной дивергенции.

Интенсивная дивергенция осуществляется так: вычисляется размер экологической ниши (a_i) первого из двух новых родов как случайное число в диапазоне от 0 до a_i предка; a_i второго нового рода - как разность a_i предка и a_i первого нового рода. Если a_i хотя бы одного из двух новых родов оказывается меньше Amin, дивергенция не происходит и род-предок сохраняется. Размер адаптивной зоны (az_i) первого нового рода вычисляется как сумма a_i этого рода и случайного числа в диапазоне от 0 до разности az_i предка и a_i первого нового рода. az_i второго нового рода определяется как разность az_i предка и az_i первого нового рода. Таким образом, процедура устроена так, что как a_i, так и az_i предка оказываются поделенными случайным образом между двумя новыми родами, причем a_i новых родов не могут быть меньше Amin, а az_i каждого рода не может быть меньше a_i этого рода.

3. Колебания размеров экологической ниши.

занимаемой родом. Модельные роды имеют постоянную величину адаптивной зоны az_i и переменный размер экологической ниши a_i. Вне зависимости от процессов дивергенции а, каждого рода может изменяться со временем. Роды могут становиться в среднем более или менее специализированными вследствие некоторых изменений внутриродовой структуры. Варьирование величины экологической ниши рода осуществляется путем прибавления к переменной a_i каждого рода на каждом шаге поправочной величины е. Предполагается, что расширению экологической ниши рода способствуют три фактора: 1. наличие значительного незанятого экологического пространства в адаптивной зоне семейства (большая величина Атах), 2. эволюционно-экологические потенции рода, определяемые, вероятно, его генофондом (большая az_i), 3. размеры уже занимаемой родом экологической ниши (большая a_i). Последняя зависимость фактически задает особую связь в процессах экологической специализации и деспециализации вида: чем меньше экологическое пространство, занимаемое родом, тем вероятнее дальнейшая специализация. Данному предположению соответствует, в частности, ряд фактов, которые обычно рассматриваются как проявление "ортогенеза": направленного возрастания специализации в ряду последовательных форм. Величина е вычисляется для каждого рода и на каждом шаге по формуле:

e = m1*(az_i - Amin)*az_i*Amax* a_i/(k1 + az_i*Amax*a_i) - (a_i -Amin)

где ml, kl - коэффициенты. Вычисляемая величина такова, что новое значение a_i не может быть меньше Amin или больше az_i.

4. Вымирание рода.

Вероятность вымирания вычисляется для каждого рода на каждом шаге. Предполагается, что вероятность вымирания узкоспециализированных родов выше, чем неспециализированных. Так, обнаруживается прямая зависимость между скоростью вымирания, вычисленной как показатель экспоненциальной линии выживания, и экспертными оценками специализированности у брахиопод и морских ежей [Марков, Наймарк, 1995а; Марков и др., 1995]. Кроме того, вероятность вымирания повышается по мере заполнения адаптивной зоны семейства. Это предположение согласуется с тем фактом, что в молодых группах, в которых еще много незаполненного экологического пространства, устойчивость родов и видов весьма высока. Также и после трансгрессий, в результате которых увеличивается величина свободного адаптивного пространства начинают появляться устойчивые роды (см. гл. 1). Иначе говоря, в те периоды, когда таксой имеет достаточно незанятого пространства в адаптивной зоне, вероятность вымирания новых родов или видов невелика и наоборот. Однако, этот механизм связи вероятности вымирания рода с заполненностью адаптивной зоны семейства не требует специального отражения в модели, поскольку он уже задан другими зависимостями. Действительно, когда Атах велика, то высока вероятность появления неспециализированных родов; в случае низкой Атах появляются в основном роды с малыми значениями az_i и a_i ; вероятность вымирания связана со степенью специализированности рода. Но может существовать и другой механизм связи Атах и вероятности вымирания рода. Принято считать (подробнее эта точка зрения обсуждается ниже), что таксоны часто вымирают вследствие прямого вытеснения со стороны других, экологически близких таксонов. Для того, чтобы отразить эту гипотезу в модели, в формулу для вычисления вероятности вымирания рода и была введена величина Атах.

Таким образом, в модели вероятность вымирания рода (Pd), при 0<Pd< 1, связана отрицательной зависимостью с величинами Атах и a_i и вычисляется по формуле:

Pd = m4 / (k4*Amax*a_i +1)

где т4 - коэффициент, определяющий верхний предел вероятности вымирания рода на каждом шаге модели, 0<m4<1, и k4 - коэффициент, определяющий форму зависимости величины Pd от специализированности рода и величины Атах.

Принятие решения о вымирании производится путем сравнения случайного числа равномерного распределения в диапазоне от 0 до 1 с Pd. Если случайное число оказывается меньше Pd, род вымирает, если больше - род сохраняется.

Рис. 12.

Схема взаимосвязей эволюционных процессов в модели: "+" -положительные связи, "-" - отрицательные. Обозначения см. в тексте

Рис. 12 иллюстрирует заданные в модели взаимодействия между тремя перечисленными филогенетическими процессами (дивергенция, специализация/деспециализация, вымирание) и пятью связанными с этими процессами переменными. Как указывалось выше, вероятность экстенсивной дивергенции (Pext) положительно зависит от размеров экологической ниши рода (a_i) и от объема свободного экологического пространства в адаптивной зоне семейства (Атах). В результате процесса экстенсивной дивергенции Атах уменьшается, а средний размер экологической ниши, занимаемой родом (а среднее), увеличивается (или, что то же самое, уменьшается средний уровень специализированности родов). Вероятность интенсивной дивергенции (Pint) отрицательно зависит от Атах. Интенсивная дивергенция приводит к появлению родов с низкими значениями a_i т.е. узкоспециализированных (а среднее уменьшается). Вероятность вымирания (Pd) отрицательно зависит от Атах и a_i. Вымирание приводит к увеличению Атах (экологическое пространство освобождается). Величина a_i (размер экологической ниши) каждого рода может меняться, причем прирост a_i положительно зависит от Атах и от самой величины a_i.

Для реализации описанной модели необходимо задать (или вычислить) следующие исходные параметры:

1) две основные константы - Az (адаптивная зона семейства) и Amin (минимальная экологическая ниша, в которой возможно существование рода).

2) четыре коэффициента, задающих среднюю скорость четырех протекающих в модели процессов: m1 (специализация - деспециализация рода), т2 (экстенсивная дивергенция), тЗ (интенсивная дивергенция), т4 (вымирание).

3) пять коэффициентов, регулирующих характер зависимости скоростей процессов от размеров адаптивной зоны и экологической ниши: kl, k2, k3, k4, k5.

4) начальные характеристики первого рода модельного семейства: az1 и а1.

Все эволюционные процессы в модельном семействе протекают далее самостоятельно, в соответствии с заданными зависимостями. Заметим, что каждый модельный таксой, так же как и реальный, характеризуется уникальным набором параметров, и этот набор является по сути количественным описанием исследуемого таксона.

На выходе модели рассматривались величины Атах и А, число субъединиц таксона, их возраст, размеры потенциальных адаптивных зон и реально занимаемых ниш, а также линии выживания субъединиц.

2.3. Некоторые замечания по поводу базовых теоретических предпосылок модели

2.3.1. Целостность модельного семейства

Данная модель основана на представлении о надвидовых таксонах как целостных биосистемах. Целостность модельного семейства заключается в том, что все роды этого семейства появляются, эволюционируют и вымирают в пределах единой адаптивной зоны семейства. Взаимодействие родов в модели (рис. 12) осуществляется через переменную Атах, которая отражает объем незанятого на текущий момент экологического пространства в адаптивной зоне семейства. Динамика всех четырех процессов, происходящих в модельном семействе, так или иначе связана с Атах. Именно в этом выражается целостность модельного семейства как системы.

Здесь следует оговориться, что, по-видимому, целостность реальных таксонов в ряде случаев обуславливается целым рядом дополнительных факторов, которые в нашей модели не учитываются: от мобильных генетических элементов и вирусного переноса генов от одного вида к другому [Красилов, 1973, 1986; Шевелев, 1977; Хесин, 1984; Кордюм, 1984; Ковалев, 1995] до межвидовой гибридизации и отношений "хищник - жертва" (см. [Одум, 1975; Красилов, 1977, 1984; Юсуфов, 1978; Любищев, 1982; Раутиан, Сенников, 1995]). В модели (как и во всей этой работе) мы ограничились рассмотрением тех механизмов, которые хотя бы в какой-то степени допускают проверку количественными методами на имеющемся в нашем распоряжении материале.

Перечислим еще раз реализованные в модели принципы, в совокупности составляющие представление о надвидовом таксоне как о развивающейся биосистеме (модельное "семейство" ниже в обобщенном виде именуется "надвидовым таксоном" или просто "таксоном", а модельный "род" - "субъединицей надвидового таксо-на" или просто "субъединицей").

1. Субъединицы надвидового таксона развиваются в пределах общей адаптивной зоны определенного объема.

2. Вероятность экстенсивной дивергенции субъединиц связана прямой зависимостью с объемом незанятого экологического пространства в адаптивной зоне таксона и обратной зависимостью - со степенью специализированности предковой субъединицы.

3. Вероятность интенсивной дивергенции субъединиц надвидового таксона связана прямой зависимостью со степенью заполненности адаптивной зоны таксона.

4. Процесс расширения экологической ниши, занимаемой субъединицей надвидового таксона (деспециализация субъединицы), связан прямой зависимостью с объемом незанятого экологического пространства в адаптивной зоне таксона; с эволюционно-экологичес-кими потенциями субъединицы (с размером ее адаптивной зоны); а также с размером уже занимаемой экологической ниши.

5. Вероятность вымирания субъединицы надвидового таксона связана прямой зависимостью с экологической специализированно-стью субъединицы, и обратной зависимостью - с объемом незанятого экологического пространства в адаптивной зоне таксона.

Обсудим по порядку каждое из этих положений.

2.3.2. Общность адаптивной зоны

Это положение представляется достаточно очевидным. Так, Э.Майр [1974] пишет: "Близкородственные виды представляют собой вариации на одну тему. Хотя каждый вид в группировке родственных видов занимает особую нишу, эти ниши в целом весьма сходны. Такие ниши являются лишь подразделениями единой "адаптивной зоны", как назвал бы ее Симпсон" (с. 411). Общность адаптивной зоны субъединиц надвидового таксона отражает тот факт, что в силу генетического родства и морфологического сходства субъединиц одного таксона они, скорее всего, будут обладать и достаточно сходными эволюционно-экологическими потенциями.

Рассматриваемое представление об общности адаптивной зоны субъединиц надвидового таксона не вызывает принципиальных возражений (хотя это довольно странно!) даже у тех авторов, которые полностью отрицают реальность надвидовых таксонов как целостных систем, как видно из следующего отрывка: "Целостность рода, семейства и других таксонов выше вида определяется уже не собственной эволюционной судьбой, как у вида, а принципиальным единством "плана строения" и образованием сходных в общем, хотя и неизбежно различных в бесчисленных мелких деталях, экологических ниш, часто в пределах одной адаптивной зоны." [Тимофеев-Ресовский и др., 1977, с. 197]. Многие авторы рассматривают общность адаптивной зоны как существенный аргумент в пользу реальности надвидовых таксонов, что видно из следующей цитаты: "С точки зрения эволюциониста, род представляет собой группу видов, происходящих от общего предка... Однако род имеет более глубокое значение. При более подробном рассмотрении обычно оказывается, что все виды, принадлежащие к данному роду, занимают более или менее определенную экологическую нишу. Таким образом, род - это группа видов, приспособленных к определенному образу жизни. Совершенно очевидно, что "родовая ниша" шире "видовой ниши", однако существуют и та, и другая." [Майр и др., 1956]. Идея о том, что целостность надвидовых таксонов определяется единством адаптивной зоны, высказывалась также В.А.Красиловым [1973, 1984, 1986], С.С.Шварцем [1980], А-П.Расницыным [1987] и рядом других авторов.

2.3.3. Ограниченность размеров адаптивной зоны

Ограниченность размеров адаптивной зоны модельного семейства (константа Az) соответствует тому, что экологические возможности любого таксона ограничены: иглокожие не выносят опреснения, млекопитающие дышат воздухом, кольчатые черви не могут летать. Организация представителей данного таксона резко ограничивает потенциальные возможности эволюционных изменений (подробнее о канализирующей роли организации см. [Иорданский, 1990, 1994]). Тот факт, что адаптивная зона любого таксона имеет границы, вполне очевиден и признается большинством специалистов. Так, в учебнике А.С.Северцова "Основы теории эволюции" [1987а, с. 275] читаем: "Наконец, сама среда (адаптивная зона), в которой протекает эволюция данного таксона... имеет обычно довольно жесткие границы, определяемые соотношением организации его особей и особей, входящих в состав таксонов, которые эволюционируют в соседних адаптивных зонах". Учение И.И.Шмальгаузена [1983] о смене форм адаптациоморфоза (от ароморфоза через алломорфоз к теломорфозу) включает в себя представление об ограниченности размеров адаптивной зоны надвидового таксона как необходимый логический элемент.

Точно измерить объем адаптивной зоны у реального таксона едва ли возможно. Но это не значит, что использовать в модели соответствующую константу - нецелесообразно. Модели для того и существуют, чтобы можно было хотя бы в первом приближении наметить подходы к решению подобных задач со многими неизвестными.

2.3.4. Вероятность экстенсивной дивергенции и объем свободного экологического пространства

Зависимости, сходные с обсуждаемой, уже использовались в ряде моделей динамики разнообразия [Rosenzweig, 1975; Sepkoski, 1991b; Maurer, 1989; Walker, Valentine, 1984]. В этих моделях скорость появления новых видов (родов) уменьшается по мере роста их числа. Хотя в перечисленных работах не делается различия между специализированными и эврибионтными видами (родами), а также между интенсивной и экстенсивной дивергенцией, а вместо совокупного объема реализованных ниш (переменная А) обычно используется просто число видов (родов), сама логика здесь и там одинаковая: экспансия таксона не может быть бесконечной, значит, нужно ввести механизм обратной связи для регуляции темпов формообразования. Вряд ли перечисленные авторы относят себя к сторонникам системной концепции надвидовых таксонов, однако они ими являются на деле. Весьма важно, что рассматриваемый механизм обратной связи в диверсификации таксона отражает принципиальное сходство в динамике развития таксонов и популяций [Sepkoski, 1991b].

Рауп [Raup, 1978] предпринял попытку рассчитать и сопоставить с действительностью вероятности вымирания некоторых семейств иглокожих и брахиопод, основываясь на данных о числе родов и скоростях вымирания этих родов. Роды в этих моделях выступали как самостоятельные, не связанные никакими взаимодействиями единицы, т.е. Рауп опирался на суммативную концепцию высших таксонов. Результаты расчетов показали почти во всех случаях более высокую модельную вероятность вымирания семейств по сравнению с реальной. На основе этого анализа Рауп сделал вывод о более высокой устойчивости реальных таксонов и существовании каких-то неизвестных механизмов, поддерживающих таксоны в устойчивом состоянии.

Можно предположить, что таким механизмом является обратная швисимость между вероятностью дивергенции вида и степенью заполненности адаптивной зоны вмещающего таксона (рода, семейства, отряда) [Sepkoski, 1991b; Марков, Наймарк, 1994в; Марков и др., 1994, 1995; Naimark, Markov, в печати]. По-видимому, плотностные взаимодействия такого рода в надвидовых таксонах могут иметь место лишь постольку, поскольку используемая классификация совпадает с реальной структурированностью адаптивных зон. Вымирание какого-либо вида, по-видимому, может стимулировать дивергенцию других видов, представляющих ту же или близкую жизненную форму, т.е. экологических аналогов; следует учитывать, что понятия "таксой" и "жизненная форма" совпадают далеко не всегда [Любарский, 1992], хотя и достаточно часто [Заварзин, 1990; Van Valen, 1971]. При прочих равных условиях все же представляется более вероятным, что освободившееся экологическое пространство займет близкородственный вид, а не экологический аналог из далекой в таксономическом отношении группы. Данный тезис основывается не только на косвенных данных и логических построениях, но и непосредственно подтверждается результатами специальных исследований [Лер, 1979; Brett et al., 1990].

Многочисленные факты из эволюционной истории различных групп организмов свидетельствуют о сравнительно высокой устойчивости надвидовых таксонов, что проявляется, прежде всего, в способности к восстановлению разнообразия после частичного вымирания.

Так, на рубеже палеозоя и мезозоя класс морских ежей вымер почти целиком: из известных родов лишь один (Miocidaris) пересек рубеж перми и триаса. От этого рода, по-видимому, произошла вся мезо-кайнозойская фауна морских ежей. Достаточно очевидно, что род Miocidaris едва ли претерпел бы столь бурную дивергенцию и дал начало десяткам отрядов и сотням родов, если бы палеозойская фауна морских ежей предварительно не подверглась вымиранию, приведшему к высвобождению огромного пространства в адаптивной зоне класса. Дивергенция рода Miocidaris, очевидно, была обусловлена не какими-то уникальными особенностями именно этого рода, а состоянием вмещающей системы, т.е. крайне низкой степенью заполненности адаптивной зоны класса.

Другие группы, почти полностью вымершие на рассматриваемом рубеже (морские лилии, мшанки, кораллы), тоже достаточно быстро восстановили прежний уровень разнообразия. В ряде случаев формы, пережившие кризисное время, были столь немногочисленны, что вовсе не оставили следа в палеонтологической летописи. Так, шестилучевые кораллы развились в мезозое от неизвестных ругоз, перешедших из перми в триас; все известные ругозы вымерли в конце перми. Быстрое восстановление прежнего уровня разнообразия произошло также во многих группах после массового вымирания на рубеже мезозоя и кайнозоя, равно как и после других, менее значительных вымирании.

Таким образом, использование в эволюционных моделях таких понятий, как "свободное адаптивное пространство" или "число незанятых ниш" представляется вполне обоснованным. Более корректной, очевидно, является первая формулировка, поскольку вторая как бы предполагает, что свободное адаптивное пространство заранее нарезано на ниши, а это далеко не очевидно (см. раздел "Терминология" во введении). В частности, это противоречило бы идее некогерентной эволюции [Красилов, 1969, 1986]. С другой стороны, в ряде случаев, по-видимому, такое предположение может быть более или менее справедливым. Об этом косвенно свидетельствуют гомологические ряды Вавилова и связанная с ними способность таксонов формировать в разных регионах и в разные геологические эпохи сходную структуру экологических ниш. Можно упомянуть в связи с этим также концепцию межзональных лакун [Каландадзе, Раутиан, 19936]. В.А.Красилов [1986] в своей теории эволюции экосистем допускает существование вакантных ниш и замечает, что это предполагает некую конечную структуру сообщества с обязательным репертуаром ниш. Тем не менее, в нашей компьютерной модели свободное адаптивное пространство является неструктурированным.

Следует отметить, что целый ряд ведущих эволюционистов использовали в своих построениях не только понятие свободного экологического пространства, но и - в той или иной форме - зависимость вероятности экстенсивной дивергенции от объема свободного экологического пространства в адаптивной зоне старшего таксона [Simpson, 1953; Stanley, 1979]. Хорошим примером может служить следующий отрывок из работы И.И.Шмальгаузена "Современные проблемы эволюционной теории" [1983, с. 332-333].

"Хомяки развивались в первой половине третичного периода только в Палеарктике. Отсюда они проникли в Северную Америку, а затем в конце третичного периода и в Африку... Хомяки застыли в Палеарктике на одном уровне организации, живя наряду с полевками и песчанками только в степных и полупустынных районах... В Северной Америке у хомяков было меньше конкурентов (были полевки и мешетчатые крысы). Они сильно размножились, дав начало многочисленным представителям Peromyscus и Reithrodontomys, которые замещают в Америке наших мышей. В плиоцене установилась связь Сев. Америки с Южн. Америкой. Хомяки проникают туда и оказываются там единственными представителями мышевидных грызунов. Они занимают ниши мышей (Eligmodontia, Hesperomys), крыс (Oryzomys), древесных крыс (Rhipidomys), полевок (Andiomys, Chinchillula), песчанок (Graomys), рыбоядных хищников (Ichthyomys, Daptomys, Rheomys) и насекомоядных (Oxymycteri)... Подобная же радиация форм при еще более быстром темпе эволюции произошла на Мадагаскаре, куда хомяки проникли только в четвертичном периоде. Так как здесь других грызунов вообще не было, хомяки сильно размножились и дали в кратчайший срок широкую радиацию форм... Эта быстрая эволюция определялась отсутствием конкурентов и обилием свободных экологических ниш, а также небольшим количеством хищников".

Из приведенного отрывка хорошо видно, что И.И.Шмальгаузен был вполне согласен с многими из базовых положений обсуждаемой модели и не видел ничего дурного в использовании понятия "свободная экологическая ниша". Да и сам пример кажется весьма убедительным: мы видим, что экстенсивная дивергенция хомяков действительно во многом определялась объемом свободного экологического пространства; отчетливо вырисовываются специфические взаимодействия между субъединицами надвидового таксона - отряда грызунов, который явственно проявляет черты целостной системы с плотностной регуляцией разнообразия.

Идеи о том, что диверсификация таксона может быть ограничена объемом доступного экологического пространства, или числом лицензий, высказывались многими авторами [Красилов, 1969; Расницын, 1987; Жерихин, Расницын, 1980; Дмитриев, 1978; Simberloff, 1972, и др.]. Рассматриваемая зависимость вероятности экстенсивной дивергенции от объема свободного экологического пространства хорошо согласуется с концепцией когерентной и некогерентной эволюции [Красилов, 1969, 1986] и адаптивного компромисса [Расницын, 1987]. Обсуждаемая зависимость отчасти соответствует распространенной точке зрения, согласно которой вероятность появления новых крупных таксонов [Мейен, 1987], эврибионтных форм [Шенборн, 1971], а также вспышек радиации [Валлизер, 1984] увеличивается при снижении давления естественного отбора. При наличии большого объема свободного экологического пространства отбор, обусловленный внутригрупповой конкуренцией, очевидно, ослаблен [Валлизер, 1984]. В собственных моделях мы предпочли воздержаться от использования таких терминов, как "пониженное давление отбора", поскольку это привело бы к ряду методологических сложностей (см. [Расницын, 19896]).

Использование понятий "свободное экологическое пространство", "свободная ниша", "лицензия" и т.п. продуктивно еще и потому, что позволяет лучше понять механизм канализирующего действия над-видовых биосистем в эволюции. По мнению В.Ф.Левченко и Я.И.Старобогатова, "это действие выражается в наличии лицензий, ограничивающих возможные границы реализованных ниш видовых популяций" [Левченко, Старобогатов, 1995, с. 71].

Еще раз оговоримся, что, используя термин "свободные ниши" или "число свободных ниш" мы не имеем в виду заранее предопределенную структурированность свободного адаптивного пространства. Данные термины здесь используются исключительно в качестве синонимов свободного экологического пространства и его объема (см. раздел "Терминология").

2.3.5. Экстенсивная дивергенция и специализированность

Используемая в модели связь вероятности экстенсивной дивергенции со степенью экологической специализированности предковой субъединицы отражает тот факт, что новые таксоны чаще происходят от неспециализированных представителей предкового таксона. Эта закономерность была сформулирована Э.Копом [Соре, 1896] и известна как правило происхождения от неспециализированных предков: "Обычно новые крупные группы берут начало не от высших представителей предковых групп, а от сравнительно неспециализированных" [Яблоков, Юсуфов, 1981, с. 229]. Неспециализированные, эврибионтные формы с большей вероятностью могут переходить в новые ниши, поскольку их адаптивная зона велика и потому контактирует с большим числом экологических вакансий; для них также характерна более высокая генотипическая и фенотипическая изменчивость. Обратная зависимость между эволюционной пластичностью вида или расы и степенью ее экологической специализации экспериментально установлена Г.Ф.Гаузе в опытах с инфузориями [Гаузе, 1984]. Эта зависимость убедительно показана также П.А.Лером [1979] в ходе анализа эволюции ктырей. Упомянем также работы А.Н.Северцова [1967], который писал: "Я не нашел примеров того, чтобы группа специализированных животных... пошла по пути прогрессивной эволюции... Насколько мы можем судить, специализация, а тем более дегенерация, служит препятствием к появлению прогрессивных изменений у животных и вступлению их на путь ароморфоза" (с. 121). К выводу о том, что "специализированные формы редко являются поставщиком эволюционного материала", пришел В.Ф.Левченко в ходе экспериментов с разработанной им имитационной моделью эволюции [1993, с. 53].

Иногда крупные апоморфии развиваются и в специализированных ветвях, но это чаще всего бывает связано с предшествующим периодом деспециализации. Например, специализированные представители рода Proraster (морские ежи) на рубеже мела и палеогена вымерли, однако в раннем палеоцене встречены первые представители рода Brisaster, которые, по всей видимости, произошли от последних Proraster путем педоморфного упрощения морфологии и экологической деспециализации. От этих форм произошла в дальнейшем разнообразная кайнозойская фауна холодноводных схизастерид [Марков, 1994].

Крупные таксоны иногда происходят от специализированных представителей предкового таксона, которые после как бы оказываются вдруг эврибионтными; это заставляет говорить об относительности понятий "специализация" и "адаптация широкого назначения" [Гиляров, 1949; Красилов, 1986; Северцов, 1984, 19876]. Изменение реального уровня специализированности при сохранении прежней морфологии и физиологии, по-видимому, может наблюдаться (и действительно наблюдается) при переходе в новую адаптивную зону. Например, предки амфибий могли бы рассматриваться как весьма специализированные кистеперые рыбы, приспособившиеся к маргинальным участкам адаптивной зоны своего таксона. Примеры подобных феноменов в эволюции морских ежей мы детально рассмотрим в главе 4. Хорошим примером может также служить снижение избирательности питания у птиц при переходе их к синантропному существованию, изученное А.А.Вахрушевым [1988].

Наша модель отчасти отражает эти явления, поскольку в ней имитируется эффект "экологического высвобождения" [Пианка, 1981]: пониженная плотность заполнения адаптивной зоны семейства (большая величина Атах) способствует увеличению реализованной ниши рода a_i. Можно было бы также предусмотреть возможность увеличения az_i рода-основателя при переходе в новую адаптивную зону. Однако мы пока ограничились моделированием эволюции таксона в пределах одного изолированного участка экологического пространства с одинаковыми свойствами во всех точках (модельная адаптивная зона не имеет внутренней структуры). В модели не предусмотрена возможность выхода за пределы этого участка, то есть дивергенции самого модельного семейства. Поэтому на данном этапе проблема относительности специализации и генерализации нас может не беспокоить; ниже мы рассмотрим этот вопрос более подробно.

2.3.6. Интенсивная дивергенция и специализация родов в связи с объемом свободного адаптивного пространства

Третья и четвертая из перечисленных в разделе 2.3.1 исходных посылок модели фактически отражают наличие конкурентных отношений, возникающих в процессе эволюции между близкородственными таксонами. Из того, что говорилось выше об общности адаптивной зоны субъединиц надвидового таксона (раздел 2.3.2), следует, что конкуренция между видами одного рода должна быть значительно острее, чем между видами разных родов. Ибо "не подлежит сомнению, что поскольку конкуренция возникает вследствие потребностей в одних и тех же источниках существования, она должна быть наиболее распространена среди особей, обладающих наиболее сходными потребностями и проявлениями жизнедеятельности" [Мазер, 1964, с. 334].

Очевидно, что во многих случаях потенциальные адаптивные зоны близких видов могут перекрываться, причем это перекрывание тем больше, чем выше степень заполненности адаптивной зоны вмещающего таксона. Растущее перекрывание адаптивных зон способствует специализации видов. Хорошей иллюстрацией этому служит явление расхождения признаков у симпатричных родственных видов (см.: [Красилов, 1977] и примеры в гл. 1). Влияние конкуренции между родственными видами на процесс специализации (сжатие и дробление ниш) подробно рассмотрел Хаксли [Huxley, 1974]; см также [Галл, 1984; Ayala, 1970, 1972; Harper, 1977]. Таким образом, возрастающая плотность заполнения адаптивного пространства надвидового таксона может вести к усилению внутренней дифференцировки и к усложнению структуры таксона за счет интенсивной дивергенции субъединиц. При уменьшении этой плотности действие стабилизирующего отбора на отдельные виды может уменьшаться, что ведет к увеличению внутривидовой изменчивости по адаптивным признакам и к деспециализации. Данное явление получило название "экологического высвобождения" [Пианка, 1981; Вахрушев, 1988]. В модели оно имитируется зависимостью изменения a_i от Атах.

С обсуждаемыми модельными зависимостями вполне согласился бы И.И.Шмальгаузен [1983], который писал: "С увеличением численности животное (имеется в виду, конечно, таксой), однако, рано или поздно сталкивалось с ограниченностью средств к жизни (ограниченность адаптивной зоны) и вступало на путь косвенной борьбы, т.е. конкуренции с себе подобными. Это ускоряло расхождение признаков, т.е. процесс дифференциации (интенсивная дивергенция). Этот процесс последовательной дифференциации имеет, однако, свой предел, диктуемый малой численностью и, следовательно, малой пластичностью дробных таксономических группировок". Предел дроблению адаптивных зон в модели задается константой Amin (минимальный объем пространства ресурсов, достаточный для существования рода). Аналогичная схема применяется, в частности, в "эвристической модели сопряженной эволюции сообщества и биоты" Н.Н.Каландадзе и А.С.Раутиана: "Предел дроблению адаптивных зон и экологических ниш, как показал В.В.Жерихин, устанавливается емкостью каждой из них, которая не может иметь ресурсов меньше того, что может обеспечить устойчивое существование в ней соответствующего таксона на протяжении филогенетически значимых отрезков времени" [Каландадзе, Раутиан, 19936, с. 86]. В той же модели применяются и зависимости, принципиально сходные с обсуждаемыми в данном разделе: "Интенсификация конкуренции и прогрессивной специализации в освоении биотической среды стимулируют, в порядке положительной обратной связи, дальнейшую специализацию..." (там же).

Заложенная в модели зависимость процессов специализации и деспециализации рода от текущей величины его специализированно-сти отражает эмпирическое "правило прогрессирующей специализации", сформулированное Ш.Депере [1876]; цит. по [Яблоков, Юсуфов, 1981, с. 228]: "группа, вступившая на путь специализации, как правило, в дальнейшем развитии будет идти по пути все более глубокой специализации". Это эмпирическое обобщение отнюдь не имеет всеобщего характера. Необходимо отметить, что и в модели соответствующая зависимость играет лишь второстепенную роль. Если убрать ее из модели, поведение модельного семейства меняется незначительно; все перечисленные ниже (раздел 2.4.5) пункты сходства с эволюцией реальных таксонов сохраняются, хотя степень сходства по некоторым пунктам несколько снижается (модель становится грубее).

2.3.7. Вероятность вымирания и специализированность

Обычно вероятность вымирания таксонов в моделях связывается с понятием приспособленности и с естественным отбором. В нашей модели приспособленность не задается и естественный отбор не имитируется. Мы разделяем мнение ряда специалистов о том, что вероятность вымирания таксона в первую очередь связана с объемом используемого "пространства ресурсов", и в значительно меньшей степени - с эффективностью его использования [Любищев, 1982; Красилов, 1984; Марков, Наймарк, 1994; Vrba, 1983]. С.В.Мейен [1987] указывал, что эволюционные новации не обязательно имеют адаптивную подоплеку, а различия в приспособленности едва ли могут сильно влиять на смену доминирующих таксонов. Вообще оценить количественно степень приспособленности, или эффективности использования ресурса у тех или иных живых организмов значительно труднее, чем степень эврибионтности [Lovtrup, 1974]. Как будет показано ниже (гл. 3), эврибионтность можно оценивать по площади ареала и продолжительности существования. Что же касается приспособленности, то мы можем лишь предполагать, что во многих случаях она повышается по мере роста специализированности и снижается при генерализации [Кафанов, 1979; Slobodkin, Sanders, 1969], однако эта связь не является ни всеобщей, ни бесспорной [Любищев, 1982]. С.Ловтруп [Lovtrup, 1974] в своей эволюционной модели вообще заменил "приспособленность" на "приспособляемость" - понятие, весьма близкое к используемой чдесь "эврибионтности" и "объему адаптивной зоны".

Данные палеонтологии убеждают нас в том, что одной из наиболее общих закономерностей таксономического вымирания является выборочное вымирание наиболее специализированных таксонов.

Идея о том, что при изменении внешних условий специализированные формы имеют больше шансов вымереть, чем неспециализированные, отнюдь не нова. Она многократно высказывалась различными специалистами начиная с прошлого века [Соре, 1896; Депере, 1915], вошла в современные учебники [Яблоков, Юсуфов, 1981; Северцов, 1987а; Шмальгаузен, 1983; Stanley, 1979] и едва ли возможно ее серьезно оспаривать. Ясно, что для вымирания стенобионтной формы достаточно небольшого изменения среды, тогда как для вымирания эврибионтной формы необходимо более сильное изменение.

Любой палеонтолог может привести немало конкретных фактов преимущественного вымирания специализированных видов, родов и семейств из эволюционной истории "своей" группы. Эти примеры можно найти в огромном множестве работ, поэтому ограничимся приведением лишь нескольких характерных фактов, связанных с вымиранием на рубеже мела и палеогена.

На рубеже мезозоя и кайнозоя из двух близкородственных отрядов морских ежей - Holasteroida и Spatangoida - первый подвергся значительно более сильному вымиранию на видовом, родовом и семейственном уровнях, чем второй (рис. 13). При всем сходстве морфологии и экологии представителей обоих отрядов, между ними имелось существенное различие: роды и виды Holasteroida в конце мела характеризовались более высоким (в среднем) уровнем специализированности, чем соответствующие таксоны Spatangoida (подробнее об этом говорится в главе 4).

Рис.

13. Морские ежи отрядов Spatangoida и Holasteroida на рубеже мела и палеогена, а - число родов, появившихся в течение сенона; б - средний индекс географического распространения (характеризует уровень неспециализированности - см. главу 3) родов, появившихся в сеноне; в - процент сенонских родов, не перешедших в палеоцен

Fig. 13.

Spatangoid and holasteroid echinoids at the Cretaceous/Tertiary boundary, a - number of genera that originated during the Senonian; б - average GDI of genera that originated during the Senonian (GDI - geographical distribution index, an estimation of the geographic range, which also reflects the degree of ecological tolerance, as discussed in Chapter 3); в - percentage of Senonian genera that are not found in Paleocene

Правильные морские ежи, представленные преимущественно эв-рибионтными, всеядными формами, подверглись на рубеже мела и палеогена значительно меньшему вымиранию, чем неправильные -преимущественно стенобионтные детритофаги.

Из всех наружнораковинных головоногих моллюсков рассматриваемый рубеж пересекли только наутилоидеи - наименее специализированная группа.

Все высокоспециализированные планктонные фораминиферы на рубеже мела и палеогена вымерли, в то время как относительно примитивные - пережили катастрофу [Корчагин, 1995, с. 62].

Из двух классов морских мшанок - Stenolaemata и Eurystomata -первый характеризуется большей специализированностью, что проявляется, в частности, в усложненной форме колоний и в строгой стеногалинности. Представители класса Eurystomata, строящие более простые колонии и способные переносить опреснение, после вымирания на рубеже мела и палеогена быстро восстановили прежний уровень разнообразия и стали доминирующей группой морских мшанок, тогда как уровень разнообразия Stenolaemata резко и необратимо сократился, и сейчас эти мшанки играют в морских сообществах весьма незначительную роль [Вискова, Морозова, 1993; Соловьев и др., 1994, 1995].

Избирательное вымирание специализированных таксонов, по-видимому, характерно не только для эпох массовых вымирании; ряд фактов свидетельствует о том, что оно происходит более или менее постоянно. Один из таких фактов - корреляция между степенью спе-циализированности родов в различных группах, определенной путем экспертных оценок, и средней продолжительностью существования родов.

Так, среди морских ежей можно выделить, в порядке возрастания среднего уровня специализации родов, пять групп: отряд Cidaroida, правильные морские ежи подкласса Euechinoidea, отряды Cassiduloida и Holectypoida, отряд Spatangoida, отряд Holasteroida, отряд Clypeasteroida. В этом ряду постепенно возрастает специализирован-ность форм: если для первой группы характерна наиболее примитивная морфология и высокая степень эврибионтности, то последняя включает крайне специализированных плоских морских ежей, или "песчаных долларов", обладающих весьма специфическими приспособлениями для просеивания песка, причем отдельные роды и виды способны существовать только в грунте со строго определенным размером частиц.

Оказалось, что средняя продолжительность существования родов в приведенном ряду закономерно снижается, а удельная скорость вымирания родов - увеличивается (рис. 14).

Рис. 14.

Коэффициент удельной скорости вымирания (доля родов, вымирающих за 1 млн. лет, если все существующие в данный момент роды принять за единицу) (а) и (б) средняя продолжительность существования родов в млн. лет у различных групп морских ежей. 1 — отр. Cidaroida, 2 — правильные ежи подкласса Euechinoidea, 3 - отр. Cassiduloida и Holectypoida, 4 -отр. Spatangoida, 5 - отр. Holasteroida, 6 - отр. Clypeasteroida

Fig. 14.

Coefficient of per unit rate of extinction of genera (ratio of genera that would become extinct during 1 min.y. to the total number of genera existing at the moment) (a) and (6) average duration of genera (min.y.) in different echinoid groups (the degree of ecological and morphological specialization increases in this row): 1 - order Cidaroida, 2 - regular echinoids, subclass Euechinoidea, 3 -orders Cassiduloida and Holectypoida, 4 - order Spatangoida, 5 - order Holasteroida, 6 - order Clypeasteroida

Аналогичные результаты получены для различающихся по уровню специализированности групп брахиопод отряда Athyridida [Грунт и др., 1995]. Та же закономерность выявлена у правильных археоци-ат [Naimark et al., 1995]: в более специализированных отрядах Capsulocyathida и Ajacicyathida средняя продолжительность существования родов меньше, чем в неспециализированном примитивном отряде Monocyathida.

Помимо экспертных оценок, степень специализированности может быть приблизительно определена по ряду косвенных показателей, например, по размеру ареала (подробнее см. гл. 3). В среднем, при прочих равных условиях, эврибионтные таксоны, очевидно, должны иметь более обширные ареалы, чем стенобионтные. Эта закономерность особенно хорошо выражена у морских организмов, в расселении которых физико-географические барьеры играют сравнительно небольшую роль. В большинстве случаев отсутствие такого-то вида в данном регионе обусловлено не тем, что вид не смог проникнуть в этот регион, а тем, что он не смог здесь прижиться по экологическим причинам. В геологическом масштабе времени расселение нового вида морского беспозвоночного в пределах потенциального ареала должно происходить практически мгновенно. Было установлено, что почти во всех случаях, когда число родов в каком-либо отряде или классе снижается, одновременно с этим увеличивается средний размер родового ареала [Марков, Наймарк, 1995а, 19956, Naimark, Markov, 1994]. Например, у палеозойских мшанок наиболее значительные вымирания на родовом уровне происходили в конце ордовика, в позднем девоне и в поздней перми; несколько менее заметное вымирание отмечается в среднем-позднем карбоне (рис. 15, а). Во всех этих случаях одновременно с вымиранием происходит значительное повышение среднеродового индекса географического распространения (рис. 15, б). Аналогичные результаты получены нами для других групп беспозвоночных: морских ежей, брахиопод, головоногих моллюсков, археоциат, кораллов (гл. 3). Во многих группах отмечается положительная связь между площадью ареала и продолжительностью существования таксона [Буко, 1979; Горюнова и др., 1994, Gorjunova et al., в печати].

Приведенные примеры, а также многочисленные литературные данные позволяют заключить, что избирательное вымирание специализированных таксонов является закономерностью общего порядка, проявляющейся более или менее постоянно.

Рис. 15.

Динамика разнообразия и размеры родовых ареалов у палеозойских мшанок, а - число родов, известных в данном веке; б - средний индекс географического распространения родов (подробнее см. главу 3)

Fig. 15.

Generic diversity dynamics and geographic ranges of genera in Palaeozoic bryozoans. a - number of genera known from the stage; б - average GDI (geographic distribution index, an estimation of geographic range) of genera

2.3.8. Конкурентное вытеснение

Реализованная в модели зависимость вероятности вымирания субъединиц от степени заполненности адаптивной зоны таксона отражает возможность прямого вытеснения одних субъединиц (видов, родов) другими. Таким образом, в модели имитируются две возможных причины вымирания:

1) колебания внешних условий, ведущие к избирательному вымиранию экологически специализированных субъединиц;

2) конкурентное вытеснение одних субъединиц другими, ведущее, очевидно, к избирательному вымиранию тех субъединиц, которые менее эффективно используют ресурс, то есть менее приспособленных, независимо от степени их специализированности.

Довольно часто высказывается точка зрения о ведущей роли прямого конкурентного вытеснения в вымирании таксонов [Давиташвили, 1969; Риклефс, 1979]; другие же авторы утверждают обратное [Красилов, 1977; Расницын, 1987; Черных, 1986].

Рассматриваемая модель позволяет (разумеется, с учетом всех заложенных в ней упрощений) дать предварительный ответ на вопрос, какая из двух возможных причин вымирания таксонов более существенна? Оказалось, что если исключить из модели возможность конкурентного вытеснения и вычислять вероятность вымирания рода по упрощенной формуле:

Pd = m4*(k4*a_i + 1)

то поведение модельного семейства практически не изменяется, и все перечисленные в разделе 2.4.5. пункты сходства эволюции модельных и реальных таксонов сохраняются. Если же исключить из модели избирательное вымирание специалистов под воздействием колебания внешних условий и оставить только конкурентное вытеснение, то есть вычислять вероятность вымирания по формуле:

Pd = m4*(k4*Amax + 1)

то поведение модели меняется коренным образом, и никакого сходства с эволюцией реальных таксонов не остается. В модельном семействе в этом случае происходит неуклонный рост разнообразия; число родов асимптотически стремится к максимально возможному (то есть к величине Атах/Атт); эпизодические небольшие снижения разнообразия не сопровождаются снижением средней специализиро-ванности родов и не стимулируют новых вспышек экстенсивной дивергенции; модельное семейство вскоре входит в устойчивое состояние гомеостаза, при котором роды предельно специализированы, а амплитуда колебаний числа родов и уровня их специализированно-сти минимальна; фаза упадка не наступает никогда.

Результаты описанного эксперимента свидетельствуют в пользу того, что избирательное вымирание специализированных таксонов под воздействием постоянно происходящих колебаний среды, по-видимому, является более общей и более важной закономерностью, чем прямое конкурентное вытеснение одних таксонов другими. Этот вывод подтверждается рядом эмпирически установленных фактов. Действительно, "вымирание крупных групп организмов, как правило, не связано непосредственно с экспансией замещающей ее в данной адаптивной зоне группы, а всегда предшествует ей. Нередко эти события разделяет перерыв, заметный даже в геологическом масштабе времени" [Черных, 1986, с. 95]. Таким образом, в подобных случаях, по-видимому, правильнее говорить именно о замещении, а не о прямом вытеснении (см. также [Родендорф, Жерихин, 1974; Расницын, 1987]).

С другой стороны, в ряде случаев конкурентное вытеснение, по-видимому, может играть существенную роль в эволюции таксонов. Обострение конкуренции может способствовать переходу отдельных групп в новые адаптивные зоны. Примеры таких процессов можно найти, в частности, в эволюции морских ежей надотряда Spatangacea (см. гл. 4) и тетрапод [Каландадзе, Раутиан, 1994]. Однако и в этом случае не всегда можно говорить о конкуренции как о непосредственной причине вымирания. По-видимому, в качестве непосредственной причины вымирания конкурентное вытеснение гораздо чаще выступает в наземных экосистемах, чем в морских (например, при соединении прежде разобщенных участков суши).

В целом, говоря о конкуренции между родственными таксонами, в большинстве случаев уместно пользоваться понятием косвенной конкуренции. Ареалы родственных таксонов далеко не всегда пересекаются, их представители могут занимать сходные ниши в пространственно разобщенных экосистемах. Поэтому непосредственно друг с другом они конкурируют редко. Однако, если в результате кратковременного изменения условий в одной из экосистем популяция какого-либо вида исчезнет или резко сократится, то представители родственных видов из соседних экосистем могут занять освободившееся жизненное пространство и тем самым воспрепятствовать восстановлению популяции "местного" вида. Такое "конкурентное вытеснение" является частным случаем более общего механизма смены доминирующих таксонов (см. гл. 5).

Таким образом, ни одна из базовых теоретических предпосылок модели не противоречит общепринятым взглядам. Однако в совокупности эти предпосылки превращают надвидовой таксой из "абстрактной категории" и "удобного средства для каталогизации видов" в целостную систему, элементы которой связаны между собой сложными специфическими взаимодействиями, отчасти напоминающими плотностные механизмы регуляции численности популяций.

2.4. Филогенез модельного семейства

2.4.1. Развитие модельного семейства в адаптивной зоне постоянного объема

Во всех модельных экспериментах основные константы (Az и Amin) полагались одинаковыми и равными соответственно 4,0 и 0,01 усл. ед. Предварительно было установлено, что ни абсолютная величина этих констант, ни их соотношение не влияют на принципиальный ход эволюции модельного семейства. Единственное условие Аz должна на несколько порядков превосходить Amin, чтобы в модельном семействе могло одновременно существовать значительное количество родов.

Оказалось, что в пределах очень большого спектра различных значений начальных параметров поведение модельного семейства относительно однообразно.

Рис. 16.

Пример развития модельного семейства: гомеостаз с чередованием фаз роста, расцвета и упадка (упадки неглубокие, реликтовая фаза не наступает), а - средняя эврибионтность родов (среднее значение a_i), б -средний возраст родов, в - объем свободного пространства в адаптивной зоне семейства (Amax), г - число родов. Начальные параметры: к1=0,005; k2=0,5; k3=5; k4=10; k5=l; ml=0,l; m2=0,l; m3=0,l; m4=0,03

Fig. 16.

An example of the development of the simulated family: a homeostasis with continuous alteration of phases of growth, acme and decline (declines are not too strong, there is no relic phase), a - average ecological tolerance of genera (average value of а,), б - average age of genera, в - volume of vacant ecological space in the adaptive zone of the family (Amax), г - number of genera. Parameters: kl=0,005; k2=0,5; k3=5; k4=10; k5=l; ml=0,l; m2=0,l; m3=0,l;m4=0,03

Исходный род дивергирует; число родов достигает некоторого максимального уровня, зависящего от параметров, после чего наступает период гомеостаза. Этот стабильный период сопровождается более или менее значительными колебаниями числа родов и длится неопределенно долгое время (рис. 16). Самопроизвольного вымирания семейства не происходит; всякий спад разнообразия рано или поздно сменяется новым подъемом. Исходные параметры определяют средний уровень разнообразия, период и амплитуду автоколебаний вокруг этого среднего значения и длительность интервала времени между появлением первого рода семейства и достижением устойчивого уровня разнообразия.

Рассмотрим более подробно процессы, происходящие в модельном семействе (рис. 17). В исходном состоянии модельное семейство представлено одним родом, который характеризуется сравнительно большими значениями az_i и а_i. Это означает, что первый род семейства обладает какой-то апоморфией, открывающей значительные эволюционно-экологические возможности (адаптацией широкого профиля); степень специализации рода низкая. В начальный момент в адаптивной зоне семейства много свободного экологического пространства [Amax велика). Это способствует высокой вероятности экстенсивной дивергенции и низкой вероятности вымирания. Следующий (второй) этап эволюции модельного семейства можно назвать фазой роста, или увеличения разнообразия. Этот этап подразделяется на два подэтапа. В течение первого из них (фаза экстенсивной дивергенции) появляются преимущественно формы с адаптациями широкого профиля, что соответствует большим значениям az_i. Фазу экстенсивной дивергенции можно сопоставить с некогерентной эволюцией по В.А.Красилову [1969, 1995] или с акцептивной фазой развития биосистем по С.В.Пучковскому [1994, 1995]. Параллельно идет и интенсивная дивергенция, в ходе которой формы постепенно специализируются. Однако в целом вновь появляющиеся роды характеризуются большими средними величинами az_i и a_i. Скорость появления родов в этой фазе максимальна и значительно превышает скорость вымирания. Число родов возрастает. Это продолжается до тех пор, пока адаптивная зона семейства не оказывается в значительной степени заполненной (Amax приближается к минимуму).

Рис. 17.

Обобщенная схема одного филогенетического цикла модельного семейства, а - число родов, б - средний возраст родов, в — объем свободного экологического пространства в адаптивной зоне семейства, г - средний размер ниши, занимаемой одним родом (средняя неспециализированность родов), д - удельная скорость появления родов, е — удельная скорость вымирания родов. Небольшие колебания в фазе расцвета происходят по тому же алгоритму, что и крупномасштабные колебания (смена фаз). Различия между этими колебаниями чисто количественные. Прочие пояснения см. в тексте

Fig.

17. Generalized scheme of a phylogenetic cycle in a simulated family, a -number of genera, б - average age of genera, в - volume of vacant ecological space in the adaptive zone of the family, r - average volume of generic niche (average ecological tolerance of genera), д - per unit rate of origination of genera, e - per unit rate of extinction of genera. The minor fluctuations during the phase of acme follow the same algorithm as the major fluctuations (the' succession of phases). The differences between these fluctuations are purely quantitative

Когда свободное экологическое пространство сужается, начинается фаза интенсивной дивергенции. Этот период характеризуется почти полным прекращением экстенсивной дивергенции; роды, возникающие в это время, в основном более специализированы, чем их предки. Средний уровень специализации родов быстро увеличивается, а Атах остается на прежнем (минимальном) уровне, поскольку интенсивная дивергенция на эту величину не влияет. Скорость вымирания родов постепенно возрастает, скорость появления снижается, но все еще превосходит скорость вымирания. Число родов продолжает расти, пока не приближается к своему максимуму. Третий этап эволюции модельного семейства можно назвать фазой расцвета (как показано в главах 3-4, при анализе эволюции реальных таксонов фазу интенсивной дивергенции удобнее рассматривать как составную часть фазы расцвета, а не фазы роста, как в этом описании, что, впрочем, непринципиально). Фазу расцвета можно сопоставить с когерентной эволюцией по В.А.Красилову [1995]. Число родов устанавливается на максимальном уровне. Скорости появления и вымирания родов примерно равны, однако новые роды появляются в основном путем интенсивной дивергенции, а экстенсивная дивергенция заторможена из-за малого объема свободного экологического пространства. Экстенсивная дивергенция во время фазы расцвета не ведет к увеличению объема занимаемого группой жизненного пространства (А) и лишь компенсирует вымирание. Средний уровень специализации родов достигает максимума. Для фазы расцвета очень характерны небольшие колебания разнообразия вокруг среднего уровня, причем средний уровень неспециализированности родов (среднее значение a_i) колеблется в противофазе с родовым разнообразием. Вымирают в основном молодые роды, поскольку они в среднем более специализированы, чем старые. В результате средний возраст родов в семействе увеличивается.

Четвертый этап эволюции модельного семейства можно назвать фазой упадка, или снижения разнообразия. Он соответствует внутреннему, или эндогенному, кризису таксона, обусловленному далеко зашедшим процессом специализации при заполненности большинства экологических ниш. Эта фаза во многом аналогична экосистемному кризису [Расницын, 1989а; Каландадзе, Раутиан, 1984, 1993а, 19936; Тимонин, 1995 и др.]. Экстенсивная дивергенция не происходит в первую очередь из-за высокой степени специализированности родов; к тому же величина Атах остается довольно низкой. Интенсивная дивергенция тоже резко замедляется, поскольку роды уже достигли высокого уровня специализации. Скорость появления родов минимальна. Скорость вымирания, напротив, максимальна, что также объясняется высокой степенью специализации форм. Число родов сокращается. Вымирают по-прежнему в основном молодые роды, в результате чего средний возраст родов увеличивается до максимума. За счет того, что вымирание затрагивает в первую очередь наиболее специализированные роды, в семействе понемногу начинается общая деспециализация. Фаза упадка продолжается до тех пор, пока в адаптивной зоне семейства не освободится такой объем экологического пространства, который достаточен для значительного замедления вымирания и возобновления процесса экстенсивной дивергенции. В зависимости от параметров моменты прекращения вымирания и начала экстенсивной дивергенции могут быть разделены более или менее длительным интервалом времени, в течение которого число родов в семействе минимально (реликтовая фаза). При значительном диапазоне начальных параметров этот период может быть весьма непродолжительным или вовсе отсутствовать.

После возобновления экстенсивной дивергенции в семействе снова появляются неспециализированные формы с адаптациями широкого профиля, и весь цикл повторяется.

Следует отметить, что фазы, проходимые модельным семейством в процессе эволюции, целиком соответствуют тем фазам, которые были выявлены в филогенезе "осредненного" семейства морских ежей надотряда Spatangacea (гл. 1), а также в филогенезе класса Regulares (археоциаты) [Naimark et al., 1995; Наймарк, Марков, 1995], палеозойских мшанок (гл. 4) и многих других групп. Основное отличие заключается в том, что реальные роды и семейства обычно (хотя и далеко не всегда) полностью вымирают в конце первого цикла. В модельном же семействе в конце фазы упадка (или после более или менее длительной реликтовой фазы) начинается регенерация. Однако при внимательном рассмотрении это различие оказывается скорее мнимым. Дело в том, что в модельном семействе регенерация происходит в результате появления неспециализированных форм с широкими эволюционно-экологическими возможностями. Будь эти модельные роды настоящими, их скорее всего отнесли бы к новому семейству, а старое оказалось бы вымершим или продолжающим существование в реликтовой фазе.

Кроме того, необычная устойчивость модельного семейства, несомненно, в значительной степени объясняется тем, что его эволюция моделируется полностью изолированно от других таксонов. Поэтому, когда во время фазы упадка большая часть адаптивной зоны семейства освобождается, это экологическое пространство остается незанятым. В природе же весьма высока вероятность того, что освободившиеся ниши будут освоены представителями других таксонов, в особенности если эти конкуренты являются неспециализированными и обладают большой эволюционной пластичностью. В этом случае семейство не сможет выйти из фазы упадка и вымрет. К тому же необходимо учитывать, что реальные надвидовые таксоны действительно обладают способностью к регенерации разнообразия после частичного вымирания. Эта способность особенно хорошо проявляется в условиях наличия обширных лакун в экологическом пространстве. В качестве примера можно привести регенерацию класса Echinoidea после вымирания на рубеже палеозоя и мезозоя, когда от единственного вьгасившего рода Miocidaris в короткие сроки произошло огромное количество новых родов, семейств и отрядов (см. гл. 5).

Наконец, при определенных исходных параметрах модельное семейство может вымереть самопроизвольно, пройдя один или несколько циклов развития (рис. 18); подробнее см. раздел 2.4.4.

Рис. 18.

Самопроизвольное вымирание модельного семейства в случае необратимости процесса специализации, а - средний размер ниши, занимаемой одним родом; б - объем свободного пространства в адаптивной зоне семейства; в - число родов. Начальные параметры: kl=0,005; k2=0,5; k3=5; k4=10; k5=5; ml=0,l; m2=0,l; m3=0,l; m4=0,03

Fig. 18.

Extinction of the simulated family without any extrinsic stimuli when the process of ecological specialization becomes irreversible, a - average volume of generic niche; б - volume of vacant ecological space in the adaptive zone of the family; в - number of genera. Parameters: kl=0,005; k2=0,5; k3=5; k4=10;k5=5; ml =0,1; m2=0,l; m3=0,l; m4=0,03

Поскольку в нашей модели надвидовой таксой представляет собой целостную систему, элементы которой связаны между собой плотностными взаимодействиями, представляется допустимым сравнение рассматриваемой модели с некоторыми моделями динамики популяций. В связи с обсуждаемой темой (кажущееся "бессмертие" модельного таксона при широком спектре входных параметров) уместно упомянуть математические модели, созданные для оценки вероятности вымирания популяции в зависимости от времени [Richter-Dyn, Goel, 1972; Hubbel, 1972; Feller, 1939]. Оказывается, специалистам в этой области тоже пришлось столкнуться с проблемой, подобной нашей. Получаемые из этих моделей зависимости показывают, что вероятности вымирания популяций обычно очень малы. Однако в более поздних работах было показано, что популяции подвергаются гораздо большему риску вымирания, если колебания рождаемости и смертности зависят в значительной мере от внешних факторов, в том числе от популяций-конкурентов [Гудмен, 1989; Бе-ловски, 1989; Leigh, 1975, 1981; Wright, Hubbel, 1983]. Эти данные вполне согласуются с приведенными выше рассуждениями. Если продолжать держаться этой аналогии, то важно и то, что влияние внешних условий усиливается во время фазы упадка, и это может ускорить вымирание модельного семейства.

Результаты реализации модели дают представление о распределении продолжительностей существования модельных родов. Линия выживания модельных родов имеет вид экспоненты (рис. 19). Стоит отметить, что продолжительности существования популяций, определяемые при помощи модельных экспериментов, также распределяются по экспоненциальному закону [Гудмен, 1989]. Очевидно, что линия выживания модельных родов должна была бы представлять cобой правильную экспоненту в том случае, если бы вероятность вымирания (Pd) являлась константой, т.е. в случае безвыборочного »ымирания родов с постоянной удельной скоростью. Однако в модели вероятность вымирания изменяется в зависимости от степени за-юлненности адаптивной зоны семейства и от степени специализированности каждого рода, что соответствует палеонтологическим фактам (гл. 1). В результате линия выживания модельных родов немного отличается от правильной экспоненты. Линия выживания, построения в логарифмической шкале по оси ординат, разделялась на отрезки, для каждого из которых строилась линия регрессии и вычислялись коэффициенты корреляции. Оказалось, что наибольшие коэффициенты корреляции получаются в том случае, если линию выживания модельных родов поделить на три неравных отрезка, соответствующие "молодым", "зрелым" и "старым" родам. Наибольшая удельная скорость вымирания характерна для молодых родов, наименьшая - для зрелых, средняя - для старых. Например, при следующем наборе исходных параметров: kl = 0,05, k2 = 0,1, k3 = 6, k4 = 20, k5 = 0,4, ml = 0,05, ml = 0,05, т3 = 1, т4 = 0,3 коэффициент удельной скорости вымирания молодых родов (возраст от 1 до 4 условных единиц времени - шагов модели) составляет -0,264 шаг^-1 при коэффициенте корреляции 0,91, коэффициент удельной скорости вымирания зрелых родов (возраст от 5 до 16 шагов) составляет -0,142 шаг^-1 при коэффициенте корреляции 0,86, коэффициент удельной скорости вымирания старых родов (возраст свыше 16 шагов) составляет -0,154 шаг^-1 при коэффициенте корреляции 0,74.

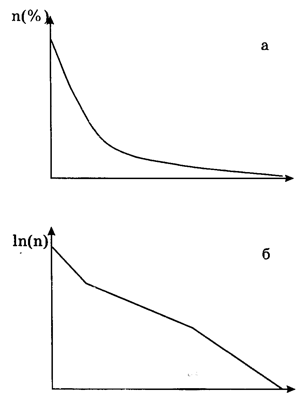
Рис. 19.

Линия выживания модельных родов. По оси абсцисс - возраст рода, по оси ординат - процент родов, доживших до такого возраста: а -обычная шкала, б - логарифмическая. Начальные параметры: kl=0,05; k2=0,l; k3=6; k4=20; k5=0,4; ml=0,05; m2=0,05; m3=l; m4=0,3

Fig. 19.

Survivorship curve of the simulated genera. Horizontal axis: age of genera; vertical axis: percentage of genera whose duration exceeded such age: a -ordinary scale, б - logarithmic scale. Parameters: kl=0,05; k2=0,l; k3=6; k4=20; k5=0,4; ml=0,05; m2=0,05; m3=l; m4=0,3

Таким образом, в модели молодые роды обладают наименьшей устойчивостью; вероятность их вымирания высока. С достижением "зрелости" вероятность вымирания снижается, а затем - снова возрастает. Эти результаты примечательны в первую очередь тем, что они полностью совпадают с данными, полученными при анализе линий выживания реальных родов и видов во многих группах беспозвоночных (морские ежи, мшанки, брахиоподы, головоногие моллюски, кораллы). Такое сходство говорит о том, что взаимосвязи, положенные в основу модели, являются адекватным и достаточным объяснением наблюдаемой в природе дифференцированной скорости вымирания разновозрастных таксонов, а именно повышенной скорости вымирания молодых и старых таксонов и пониженной скорости вымирания зрелых таксонов. Наибольшую роль, по-видимому, здесь играет зависимость вероятности вымирания таксона от степени его экологической специализированности.

2.4.2. Реакция модельного семейства на увеличение адаптивной зоны (Az)

Модель позволяет имитировать природные процессы, приводящие к увеличению потенциальной емкости среды в отношении данного таксона. Для бентосных животных такими процессами могут быть, например, потепления, трансгрессии и увеличение площади теплых мелководных морей. Для моделирования подобных событий использовался следующий прием: величина Az (адаптивная зона семейства) в какой-то момент увеличивалась, например, в 2 раза, и далее сохранялась на этом новом уровне.

Независимо от того, в какой фазе эволюционного Цикла (роста, расцвета, упадка или реликтовой) находится модельное семейство в момент увеличения Az, расширившаяся адаптивная зона стимулирует процесс экстенсивной дивергенции. Фактически семейство вступает в фазу экстенсивной дивергенции со всеми ее характерными признаками. Появляются формы, в среднем менее сПбЦИ^изированные, чем их предки; многие из вновь появляющихся родов обладают адапта-циями широкого профиля; число родов быстро возрастает; специализация идет медленно или не идет вовсе.

Когда адаптивная зона семейства вновь оказывается почти заполненной, начинается фаза интенсивной дивергенции, затем - расцвет, упадок и т.д. Естественно, теперь колебания числа родов будут происходить вокруг нового (большего) среднего уровня.

2.4.3. Реакция модельного семейства на усиление внешних истребляющих воздействии (моделирование экзогенных кризисов)

Известно, что в эволюции большую роль играют массовые вымирания, вызываемые внешними причинами (похолодания, регрессии, уничтожение огромных площадей литорали и шельфа в результате соединения континентов, падение крупных метеоритов, резкая активизация вулканической деятельности и т.д.). В модели подобные события имитировались путем временного увеличения вероятности вымирания (Pd).

Оказалось, что влияние экзогенного кризиса на эволюцию модельного семейства очень сильно зависит от того, в какой фазе филогенетического развития находится семейство в момент кризиса. Рассмотрим сначала случай, когда семейство находится в фазе расцвета или упадка (рис. 20а). В это время специализация форм высока, а процесс экстенсивной дивергенции приостановлен. Экзогенный кризис в этом случае приводит к вымиранию большой части модельных родов. Семейство может быть преждевременно ввергнуто в глубокий упадок. Экзогенный кризис как бы накладывается на приближающийся или уже наступивший эндогенный кризис и значительно усиливает его эффект. Число родов сокращается сильнее, чем при воздействии одного лишь эндогенного кризиса. Часто после этого наступает длительная реликтовая фаза, во время которой судьба модельного семейства во многом зависит от фактора случайности, поскольку число родов очень мало. Начало регенерационных процессов может задержаться на длительный срок. Наступивший в фазе расцвета или упадка экзогенный кризис приводит к преимущественному вымиранию молодых родов. Эта особенность, как и другие аспекты поведения модельного семейства в рассматриваемом случае, совпадает с реальными фактами, имевшими место в геологическом прошлом. Так, очень похожее поведение характерно для многих так-сонов бентосных животных во время кризиса на рубеже мела и палеогена [Соловьев и др., 1994, 1995], когда во многих таксонах был велик процент узкоспециализированных форм. Как отмечалось выше, у морских ежей во время этого кризиса молодые роды вымерли сильнее, чем зрелые и старые (гл. 1). Сходство дополняется еще и тем, что восстановление разнообразия у морских ежей, как и у многих других групп, началось не сразу после кризиса, а лишь в эоцене. Палеоцен же представляет собой своеобразный период застоя и характеризуется сравнительно низким уровнем разнообразия [Москвин и др., 1980; Алексеев, 1984; McKinney et al., 1992].

Рис.

20. Реакция модельного семейства на одномоментное усиление внешних истребляющих воздействий (экзогенный кризис). По оси абсцисс -время (усл. ед.), по оси ординат - число родов. Стрелкой обозначен момент кризиса, а - кризис застает семейство в фазе упадка, б - в фазе роста. Сила воздействия в обоих случаях одинакова

Fig. 20. The reaction of the simulated family to the momentary increase of extrinsic exterminating factors (exogenous crisis). Horizontal axis: time; vertical axis: number of genera. The moment of the crisis is marked by the arrow, a — the crisis occurs when the family is in the phase of decline, б - in the phase of growth. The strength of the impact is the same in both cases

Рассмотрим теперь случай, когда экзогенный кризис застает модельное семейство в фазе экстенсивной дивергенции, (рис. 206). В этой ситуации влияние кризиса оказывается менее заметным. Уровень специализированности форм невысок, поэтому снижение числа родов в результате кризиса оказывается менее значительным или даже вовсе не происходит. Кроме того, благодаря активно идущему процессу экстенсивной дивергенции, который в результате частичного вымирания только ускоряется, происходит быстрая компенсация последствий кризиса. Прежнее число родов быстро восстанавливается и продолжает расти. Примечательно, что экзогенный кризис, заставший род в фазе экстенсивной дивергенции, не приводит к преимущественному вымиранию молодых видов. Напротив, молодые виды обычно страдают меньше, чем старые, поскольку они в среднем менее специализированы.

Совершенно так же воздействует экзогенный кризис на модельное семейство в том случае, когда непосредственно перед кризисом Произошло улучшение условий (Az увеличилась). Это объясняется тем, что увеличение Az, как уже говорилось, приводит к вступлению семейства в фазу экстенсивной дивергенции независимо от того, в какой фазе оно находилось до этого.

Можно заметить, что в данном случае модельное семейство ведет себя точно так же, как реальные таксоны. Например, во время кризиса в конце сеномана, наступившего сразу после альб-сеноманской трансгрессии, молодые роды морских ежей вымерли в меньшей степени, чем зрелые и старые (гл. 1). Последствия сеноманского кризиса были быстро скомпенсированы последующим увеличением разнообразия [Соловьев и др., 1994]. Аналогичная ситуация наблюдалась в силуре у мшанок и брахиопод [Марков и др., 1995]: период повышенной устойчивости молодых родов совпадает с увеличением площади теплых мелководных морей и с высвобождением обширного экологического пространства после массового вымирания на рубеже ордовика и силура. Повышение устойчивости молодых родов имело место также у мшанок во время предполагаемой трансгрессии в начале карбона.

Яркий пример того, насколько по-разному может влиять изменение внешних условий на таксоны, находящиеся в разных фазах филогенетического цикла, дает эволюционное развитие мшанок отряда Trepostomida (см. гл. 4). Этот отряд в конце ордовика был представлен двумя основными подотрядами: Halloporina и Amplexoporina. Представители этих подотрядов были весьма сходны по морфологии и экологии, но сами подотряды находились в разных фазах филогенеза. Первый подотряд находился в стадии расцвета; новые роды в нем появлялись преимущественно интенсивным путем, были узкоспециализированными и имели маленькие ареалы. Второй подотряд переживал фазу экстенсивной дивергенции: роды, появлявшиеся в этом отряде, отличались низкой специализированностью и обычно имели обширные ареалы. На рубеже ордовика и силура, возможно, в результате произошедшего тогда крупного оледенения, подотряд Halloporina подвергся массовому вымиранию, которое продолжалось также и в силуре. В подотряде Amplexoporina в это же время число родов не только не сократилось, но продолжало неуклонно расти.

2.4.4. Входные параметры модели и их влияния на поведение модельного семейства

В ходе экспериментов с моделью было установлено, что для того, чтобы получить все возможные варианты развития модельного семейства, не обязательно изменять все входные параметры. Оказалось, что вполне достаточно экспериментировать только с четырьмя параметрами: k5, m2, т3, т4. В экспериментах, результаты которых описаны ниже, все остальные параметры были фиксированы (k1 = 0,005; k2 = 0,5; k3 = 5; k4 = 10; m1 = 0,1).

Попробуем охарактеризовать биологический смысл оставшихся четырех параметров.

Параметр k5 определяет, насколько сильно вероятность экстенсивной дивергенции зависит от специализированности рода-предка. Это, таким образом, количественное выражение "правила неспециализированного предка".

Параметр m2 задает "фоновую" скорость (вероятность) экстенсивной дивергенции, то есть что-то вроде базового уровня эволюционной пластичности. Чем выше значение m2, тем выше пластичность. Это может соответствовать, например, "универсальности" или "перспективности" плана строения, или, скажем, средней или общей "преадаптированности" представителей данного таксона к обитанию в областях пространства ресурсов, близких к той, в которой они возникли.

Параметр т3 задает фоновый уровень интенсивной дивергенции -степень выраженности тенденции к дроблению ниш. Эта тенденция, вероятно, сильнее выражена у доминирующих групп, чем у подчиненных; у виолентов - сильнее, чем у патиентов и эксплерентов, и т.д. (подробнее см. главы 4-5).

Параметр т4 задает фоновый уровень вымирания и, по-видимому, вполне соответствует понятию стабильности/нестабильности внешних условий.

Изменяя эти четыре параметра, можно получить три основных варианта поведения модельного семейства:

1) Первый род семейства вымирает, не успев дивергировать, реже делится интенсивным путем на 2-3 рода, которые сразу же вымирают. Это происходит, естественно, в том случае, когда фоновый уровень вымирания слишком высок, а фоновые скорости интенсивной и экстенсивной дивергенции слишком низки. В этой ситуации развитие модельного семейства большого теоретического интереса, очевидно, не представляет.

2) Развитие семейства протекает в соответствии с приведенным в пункте 2.4.1 описанием: наступает своего рода гомеостаз с бесконечным чередованием фаз экстенсивной дивергенции, расцвета и упадка (рис. 16). Такое развитие модельного семейства наиболее типично (соответствует самому широкому спектру входных параметров, при которых не происходит моментального вымирания семейства).

3) Семейство полностью вымирает в конце первой или, реже, второй - третьей фазы упадка.

Развитие второго типа происходит, например, при следующем наборе параметров: k5 = 1; т2 = 0,1; тЗ = 0,1; т4 = 0,03 (рис. 16).

Уменьшение роли "правила неспециализированного предка" (k5 = 0,5 и менее) приводит к снижению амплитуды колебаний разнообразия, в пределе (k5 = 0) - к гомеостазу почти без всяких колебаний при высокой степени специализации родов. Семейство вступает в вечную фазу расцвета, фаза упадка никогда не наступает (рис. 21 а).

Чем больше мы верим в закон Копа (k5 = 2 и более), тем больше амплитуда колебаний разнообразия, тем выраженное периоды упадка и последующие вспышки экстенсивной дивергенции. При k5 = 5 происходит самопроизвольное вымирание семейства в конце первого филогенетического цикла (первый же упадок оказывается настолько глубоким, что заканчивается полным вымиранием: рис. 18). Таким образом, в рамках нашей модели действенность правила неспециализированного предка является необходимым условием наступления фазы упадка и самопроизвольного вымирания семейства. Если принять точку зрения А.С.Северцова [19876], который отрицает упомянутое правило, то следует признать, что упадок таксона может быть вызван только внешними факторами.

Если усилить тенденцию к дроблению ниш (тЗ = 0,5), то самопроизвольное вымирание семейства будет происходить уже при k5 = 3, то есть при более слабой зависимости эволюционной пластичности от специалйзированности. Таким образом, повышенная тенденция к дроблению ниш может являться дополнительным фактором, способствующим наступлению упадка и даже полному самопроизвольному вымиранию таксона. Этот факт хорошо согласуется с моделью смены доминирующих таксонов, изложенной в гл. 5: в доминирующем таксоне острее внутригрупповая конкуренция, что создает предпосылки для дробления ниш, а это, в свою очередь, повышает вероятность вымирания таксона (особенно в случае резкого изменения внешних условий).

Рис. 21.

Динамика родового разнообразия в модельном семействе при различных значениях начальных параметров. Во всех трех случаях kl=0,005; k2=0,5; k3=5; k4=10; ml=0,l. a - не действует "закон Копа" (k5=0; m2=0,l; m3=0,l; m4=0,03); б - исключена возможность освоения новых ниш (нулевая эволюционная пластичность: k5=l; m2=0; m3=0,3; m4=0,03); в - сильная тенденция к дроблению ниш при сильном фоновом вымирании (доминирующий таксой в нестабильной среде: k5=l; m2=0,1; m3=0,9; m4=0,2)

Fig. 21.

The dynamics of generic diversity in the simulated family under different values of initial parameters. In all three cases: kl=0,005; k2=0,5; k3=5; k4=10; ml =0,1. a - the "Cope's law" does not work (the specialized genera are no less likely to produce new genera than eurybiontic ones: k5=0; m2=0,l; m3=0,l; m4=0,03); б - the occupation of the new niches is impossible (zero evolutionary plasticity: k5=l; m2=0; m3=0,3; m4=0,03); в - strong tendency for splitting of the niches combined with high level of background extinction (dominant taxon in unstable environment: k5=l; m2=0,l; m3=0,9; m4=0,2)

Любопытно, что усиление фонового вымирания родов (параметр т4) отнюдь не способствует самопроизвольному вымиранию семейства. Напротив, увеличение параметра т4 ведет к снижению средней степени специалйзированности родов, поскольку роды с низкими значениями a_i сразу же вымирают. В результате в семействе накапливаются эврибионтные устойчивые роды, для которых характерна высокая вероятность экстенсивной дивергенции (высокая пластичность). Такое семейство весьма устойчиво, несмотря на низкое родовое разнообразие. Дальнейшее увеличение параметра т4 может, конечно, привести к тому, что первый род семейства вымрет, не успев дивергировать экстенсивным путем. Если же экстенсивная дивергенция успеет начаться, модельное семейство будет в течении неопределенного времени оставаться "ювенильным таксоном" [Ковалев, 1994], состоящим из небольшого числа эврибионтных устойчивых родов. Поскольку параметр т4, как мы уже отмечали, соответствует уровню нестабильности внешних условий, данный результат следует рассматривать как подтверждение (или объяснение) известной закономерности: в нестабильных условиях специализация не происходит [May, McArthur, 1972;Вахрушев, 1988].

В целом можно заключить, что в рамках данной модели самопроизвольное вымирание надвидового таксона возможно только в случае необратимости процесса специализации. Такая необратимость может быть обусловлена резким снижением эволюционной пластичности у специализированных форм в сочетании с достаточно сильной тенденцией к дроблению ниш (например, в доминирующих так-сонах). К сожалению, на основании одних лишь модельных построений мы не можем оценить вероятность самопроизвольного вымирания реальных таксонов. Можно лишь констатировать, что используемая система гипотез (см. раздел 2.3) не исключает такой возможности. Это само по себе очень интересно, поскольку мы, таким образом, пользуясь одними лишь общепризнанными (по крайней мере, не противоречащими общепризнанным) положениями показали возможность таких явлений, как старение и самопроизвольное вымирание надвидового таксона.

Тем не менее, наблюдаемое закономерное вымирание реальных родов и семейств, а также многих отрядов и некоторых классов в конце фазы упадка скорее всего объясняется косвенной конкуренцией со стороны других групп, представители которых способны быстрее занимать освобождающиеся участки экологического пространства. В роли "вытесняющих", или, точнее, "замещающих" групп чаще всего выступают близкородственные таксоны.

Уменьшение параметра т2 ("базовая пластичность") не дает заметного эффекта. Только если положить т2 = 0, происходит самопроизвольное вымирание семейства. Это, однако, совершенно немыслимая в природе ситуация (рис. 216). Если бы живые организмы имели нулевую эволюционную пластичность, то эволюции не было бы вовсе. Любопытно, что для поддержания гомеостаза достаточно крайне низких значений т2. Нормальное развитие модельного семейства, таким образом, происходит даже в том случае, если вероятность появления адаптации широкого профиля и выхода в новую область адаптивного пространства крайне мала (но все же не нулевая).

Увеличение параметра т2 дает тот же эффект, что и отрицание закона Копа (уменьшение k5): все лакуны мгновенно заполняются, фазы упадка слабо выражены или вообще не наступают. Для семейства в этом случае характерны слабые колебания родового разнообразия и сильная специализация родов. Последний эффект может быть снят путем увеличения фонового вымирания (параметр т4).

Уменьшение параметра тЗ (тенденция к дроблению ниш) не меняет "типичного" хода эволюции модельного семейства. Наблюдается снижение среднего уровня родового разнообразия и средней спе-циализированности родов; последовательность фаз сохраняется. Эффект, даваемый снижением тЗ, как ни странно, может быть полностью снят увеличением т2. Так, при тЗ = 0 и т2 = 1 (интенсивная дивергенция вообще не происходит, вероятность экстенсивной дивергенции очень высока) поведение модельного семейства мало отличается от исходного. Это связано с тем, что заложенный в модели механизм экстенсивной дивергенции сам по себе достаточен для того, чтобы в семействе воспроизводилась "правильная" динамика специализированности. По мере сокращения свободного пространства в адаптивной зоне семейства роды, появляющиеся экстенсивным путем, неизбежно становятся все более специализированными, поскольку на их долю остается все меньше пространства. Хотя непосредственного дробления ниш и не происходит, конечный результат оказывается таким же, как и при действии механизма интенсивной дивергенции. Старые эврибионтные роды рано или поздно вымирают, а новые роды становятся все более специализированными. Однако для того, чтобы экстенсивная дивергенция могла компенсировать отсутствие интенсивной дивергенции, значение параметра т2 должно быть очень высоким. А это практически исключает возможность самопроизвольного вымирания и даже сколько-нибудь глубокого упадка.

Одновременное резкое увеличение параметров тЗ и т4 прибли-чительно соответствует развитию "очень доминирующей группы" в "очень нестабильных условиях". При этом наблюдаются резкие, почти хаотические колебания родового разнообразия с большой частотой и амплитудой и очень высокий темп обновления родового состава (рис. 21 в). Это, вероятно, может отчасти соответствовать развитию господствующих групп, представители которых занимают верхние трофические уровни (аммониты, например).

В заключение отметим, что все основные свойства модели, описанные в разделах 2.4.1-2.4.4, сохраняются и в том случае, если исключить из нее зависимость вероятности вымирания родов от заполненности адаптивной зоны семейства (Pd от Атах, что соответствует непосредственной плотностной регуляции разнообразия) и оставить только зависимость Pd от a_i, (избирательное вымирание специализированных). Хотя, безусловно, вероятность вымирания связана с объемом свободного экологического пространства опосредованно, через специализированность появляющихся субъединиц.

2.4.5. Сравнение с эволюцией реальных таксонов

Как мы видели, эволюция модельного семейства обнаруживает большое сходство с эволюцией реальных таксонов как в спокойные периоды, так и во время резких колебаний внешних условий. В целом сходство эволюционного развития модельных и реальных таксонов проявилось в следующем:

1. В филогенезе модельных и реальных таксонов выделяются сходные фазы (экстенсивной дивергенции, интенсивной дивергенции, расцвета, упадка, реликтовая); динамика разнообразия в общем случае описывается куполообразной кривой.

2. Влияние экзогенных кризисов на эволюцию как модельных, так и реальных таксонов, зависит от фазы филогенеза: во время фазы расцвета или упадка это влияние максимально, во время фазы экстенсивной дивергенции - минимально.

3. Линии выживания как модельных, так и реальных родов обычно состоят из трех частей, характеризующихся различными значениями коэффициента удельной скорости вымирания.

4. Отмечается сходная избирательность вымирания в модельных и реальных таксонах как в спокойные периоды, так и во время кризисов.

Другие важные аспекты сходства модели с реальностью рассматриваются в главах 3-4.

Анализ модели показывает, что зависимости, положенные в ее основу (они обсуждались в разделе 2.3), могут служить одним из возможных объяснений некоторых закономерностей эволюции, которые не были непосредственно заложены в модель (прежде всего -смены фаз филогенеза и зависимости устойчивости таксона к колебаниям внешних факторов от фазы развития). Это дает основания предполагать, что имитируемые в модели взаимосвязи между эволюционирующими субъединицами надвидового таксона в той или иной степени действительно проявляются в живой природе.

Чтобы предлагаемая модель имела реальную прогностическую ценность или отвечала иным задачам количественного анализа, необходимо разработать методику оценки параметров этой модели. Для этого необходимо тщательное изучение процессов и зависимостей, положенных в основу модели, на конкретном и разнообразном палеонтологическом материале.